(Edit: a previous version of this article stated that players with similar Elo were paired by the GEM system. This was a miscommunication regarding the article content and is not the case. Rounds are paired by the GEM system as specified by the Pairings and Tiebreaker Policy)
The Elo ranking system is a way to quantify the relative strength of each player based on their record of play over competitive history in Flesh and Blood. Each player has Elo ranking, which is a number that goes up when they win games, and goes down when they lose games. Players start at the prescribed ranking of 1500 and the amount that the ranking goes up and down depends on their opponent's ranking at the time the game was played.
Elo ranking is used to determine who are the strongest players in the world. The benefit it has over XP is that a player can achieve and maintain a high Elo ranking without having access to many competitive tournaments. While Elo does take some time to adjust players to their approximately correct rankings, it is a robust and tested system widely used in many other competitive games.
How does Elo work?
The Elo ranking of a player only makes sense in the context of comparison. When you compare two rankings, you can estimate the outcome of a match between the two players with those rankings. A player's expected score is essentially the probability of that player winning (although there's a little more to it than that). For simplicity we can just assume that a match win has a value of 1, a loss has a value of 0, and a draw has a value of 0.5. The expected score is a fractional value between 0 and 1 and the expected score for both players sum up to the value of 1 (as only there is one match to win between the players). The expected score is calculated using the following equation:
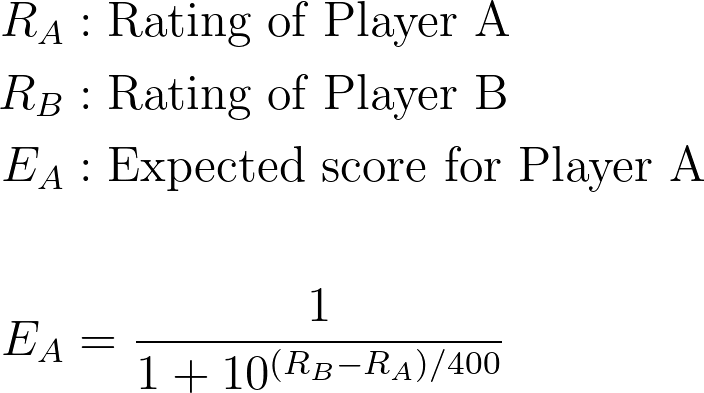
It’s important to note that the expected score is never exactly zero or one. There’s always a tiny chance, no matter how small, that a player may win or lose even if the difference between the rankings of the players is large. Here is a small example of what the expected score is for a player based on how their ranking compares to their opponent:
| Ranking difference | -800 | -400 | -200 | -100 | -50 | 0 | 50 | 100 | 200 | 400 | 800 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Expected score | 0.01 | 0.09 | 0.24 | 0.36 | 0.43 | 0.5 | 0.57 | 0.64 | 0.76 | 0.91 | 0.99 |
Once you have the expected score for each player, and the match has been completed, you can adjust each player’s ranking based on whether they overperformed or underperformed against their expected score. The adjustment is calculated using the following equation:

Depending on the expected outcome, the adjustment can be small or large. The greater the difference between the expected score and the actual score, the greater the change in ranking. The actual calculation that FaB uses for draws is slightly different and can be found here in the Ratings Policy.
What does the k-value mean?
The k-value is essentially a way to moderate how fast a player’s rating changes. To make it easier to understand, think of it like this: the k-value is the maximum Elo rating you can gain or lose for any match you play. So if the k-value is 32 and you have a rating of 1500, the range of your rating after playing a game can be anywhere from 1468 to 1532.
I need a real example!
No worries! Let’s look at an example tournament with a k-value of 32. Say we have the following players (with their Elo rankings in brackets):
- Tyler (1500)
- Nic (1400)
- Sam (1900)
- Jo (1550)
First, let’s put Tyler against Nic, and Sam against Jo. Based on their relative rankings, Tyler and Nic’s expected scores are 0.64 and 0.36 respectively, and Sam and Jo’s expected scores are 0.89 and 0.11 respectively. You can see that the expected score for Tyler and Sam are higher than their opponents because they have a higher ranking (we expect them to have a higher chance to win).
From this and the result of the game, we can calculate how much we change each player’s ranking if they win. Let’s say Tyler wins against Nic, and Jo wins against Sam. The
Change in the rating is calculated as the difference between the expected and real score multiplied by the k-factor.
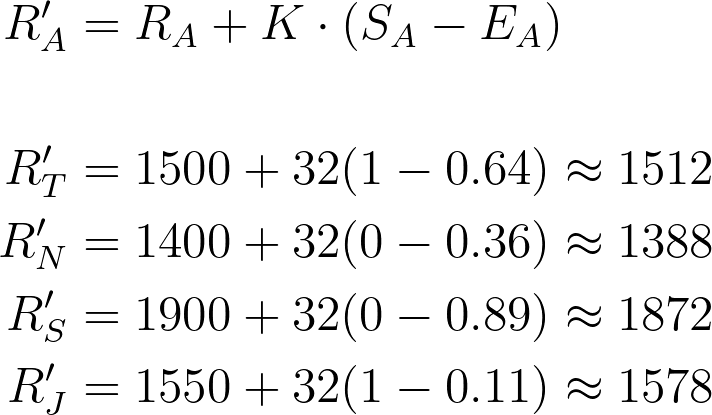
- Tyler (1512) [+12 for winning]
- Nic (1388) [-12 for losing]
- Sam (1872) [-28 for losing]
- Jo (1578) [+28 for winning]
Pair the winners together and the losers together, then play another round, we have Tyler and Jo with expected scores of 0.41 and 0.59, and Nic and Sam with expected scores of 0.06 and 0.94. If Tyler and Jo draw, and Sam wins against Nic, we have the following new ratings:
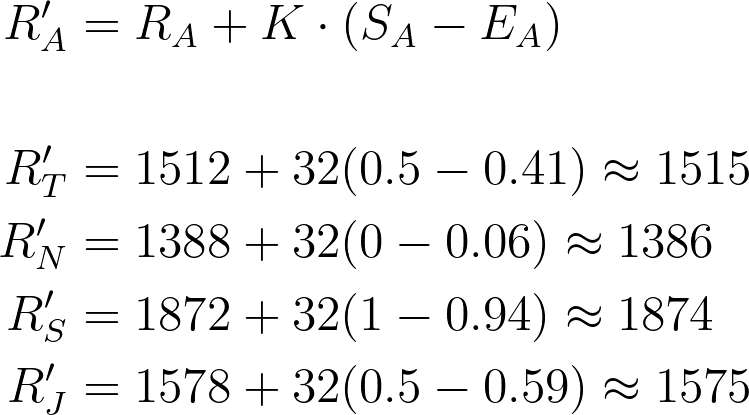
- Tyler (1515) [+3 for drawing]
- Nic (1386) [-2 for losing]
- Sam (1874) [+2 for winning]
- Jo (1575) [-3 for drawing]
You can see here that the expected scores for each match are very close to the real scores that happened. As such there are only minor adjustments for each player’s ranking.
My friend went 3-0 and I went 2-1, and they got 3 times the Elo increase. What happened?
This is an example of how cumulative updates to Elo work. Unlike XP which is simply the sum of positive values, Elo can go up and down depending on the results of your games. For example, if you win three games and you might gain 10 points from each towards your ranking, which is a total increase of 30. However, if you win two games and lose one, you might gain 10 points from the games you win and lose 10 from the game you lost, resulting in a total increase of 10 points overall (10 + 10 – 10). Compare this to XP, where if you win three games at 3XP a piece, you’ll have an increase of 9XP, but if you win two and lose one, you’ll have an increase of 6XP (3 + 3 + 0).
I went 2-1, but my Elo went down overall. What happened?
This is an example of what can happen when you only play against players of a lower ranking than you. The number of rating points you lose against a lower-ranked player is significantly greater than the amount you gain by winning against other lower-ranked players.
Here is an example. You are playing at a tournament with a k-factor of 32. If you are ranked at 2000, and you win two games against players ranked 1600, then lose to a player ranked at 1600, your score would increase by approximately 3 for each game won and then decrease by 29 for the game lost. At the end of the tournament, you see that your Elo ranking is now 1977 (2000 + 3 + 3 – 29). This is because the system has adjusted your Elo based on the expected score between the players given their starting Elo. With a higher Elo, you’re expected to win more games against players with lower Elo.
Note that the reverse is also true. If you start with a lower Elo and play against higher-ranked players, you will see a significant increase in Elo points for each win, even if you lose more games overall.
My ranking has gone up and down by exactly 16 every game. What happened?
In many regions around the world, players will be playing at an Elo-ranked tournament for the very first time. Because players start at an Elo ranking of 1500, if these players are matched in every round of the tournament the expected score for both players is calculated to be approximately 0.5 every round.
For example, let’s say you’re playing at an Elo-ranked tournament with a k-value of 32, and everyone there hasn’t played an Elo-rank match before. You start round 1 with a ranking of 1500 and you’re paired against another player with a ranking of 1500 (estimated score of 0.5). You win the game and your ranking increases to 1516 (+16). In round 2, you’re paired against another player in the same position (started with 1500, and won their first game) who has the same ranking of 1516 (estimated score of 0.5). You win the game and your ranking increases to 1532 (+16). In round 3, you’re paired against yet another player with the same record (2-0) and ranking of 1532 (estimated score of 0.5). This pattern continues for the duration of the tournament, and unless there is a situation where you are paired against a player with a different Elo ranking, your ranking will only ever increase or decrease by 16.
I just played a game/tournament and my Elo ranking hasn’t updated. What happened?
The updates for Elo rankings are done in batches to ensure that the results of games and/or tournaments, in general, have a window of opportunity to correct any match results that were input incorrectly. Retroactively recalculating Elo rankings is an issue that we would like to avoid as small change has increasing knock-on effects for every subsequent ranking calculation. As such, ensuring that the calculation is done correctly the first time (based on the correct information) is more important than calculating an intermediate result that may change if an error is caught later on. This means that you may not see updates to your Elo ranking until a batch of match results has been processed.
The Future of Elo
The Elo ranking system is the current system for evaluating the relative strength of players. It is a tried and tested system that has been used for numerous competitive games and makes a significant step forward in recognizing the players that have consistent successful performance at the highest levels of competitive play.
Elo is the system we currently use, but that might not always be the case. As will all of our systems we are constantly updating our policies and striving to maintain our philosophy of bringing people together in the flesh and blood through the common language of playing great games. As such we are already well aware of the limitations that Elo may have when it comes to maintaining that philosophy at the highest levels of play and will be monitoring the progress of players closely to ensure that the system is working as intended.